Simple Modifications

Simple Mods are designed to reuse (copy, mirror, replace) one of the (or all) parts of mixed attack generated before the mod. Part to use can be set as: 0 - all prior parts. -1 - preceding part. 1,2,... - first, second, etc. (applicable to add copy / reverse only). Simple Mod is applicable to brute-force, dictionary, multi-position mod or fixed parts. Simple mod can be applied to a simple mod as well.
ab + cd + CopyAll = abcdabcd. (add all)
ab + cd + RevAll = abcddcba. (add all in reverse)
ab + cd + CopyP1 = abcdab. (add part 1)
ab + cd + =RevP-1 = abdc. (reverse preceding part)
ab + cd + Sub[a4b6] = 46cd. (substitute chars)
"Restart password" is a special option for advanced setups. It hides all prior parts, but the parts are still available to be copied into the final output. The option can be employed to reorder attack output or to pre-generate part(s) with multiple modifications applied.
BF[1]"0..9" + BF[1]"A..Z" = 0A, 0B, 0C, 0D, ... 0Z, 1A, ... , 9Z
BF[1]"A..Z" + BF[1]"0..9" + Restart + CopyP2 + CopyP1 = 0A, 1A, 2A, 3A, ... 9A, 0B, ..., 9Z
pass + * + MPmov + Restart + BF[1]"0..9" + CopyP3 = 0*pass, 1*pass, ... 9*pass, 0p*ass, ..., 9pass* Search range can be narrowed or broadened with the following options:
Pass unmodifiable - pass unmodifiable input (empty part to copy, no chars to substitute, etc.)
Try with and without - check modified version before unmodified.
Filter unmodifiable - filter unmodifiable input.

Example:
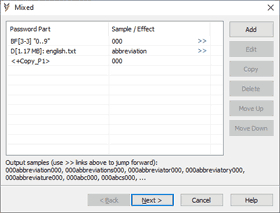
Let's say there are 3 parts in your password: 3 digits + word + 3 digits in reverse, like "123pass321".
Complexity for this attack without simple mod (3 chars "0..9" block + dictionary + 3 chars "0..9" block) is equal to 1000 * (num. of words in the dictionary) * 1000.
3 parts mixed attack:
<numbers> - brute-force, 3 chars, "0..9" charset. <word> - dictionary file. +RevP1 - Simple Mod: part 1 copied in reverse. Complexity for the modified version (1 block of 3 chars "0..9" + dictionary + Mod) is equal to just 1000 * (num. of words in the dictionary), thus this setup is 1000 times faster!